V té čtvrté zatáčce to není náhoda. Odhad rychlosti a poloměru zatáčky selhává přesně ve chvíli, kdy je přesnost přistávacího manévru nejvíce potřebná pro bezpečné přistání.
Závěrečnou čtvrtou zatáčkou se dotáčíme se do osy přistávací dráhy a provádíme ji v malé výšce. Když jsem létal plachtařský výcvik, jako každý žák jsem dělal stejnou chybu. Měl jsem tendenci v blízkosti země zatáčku točit s malým náklonem. Klesala mi rychlost, s přehnaně vyšlápnutou směrovkou a kuličkou zahnanou do rohu jsem si ve výkluzové zatáčce koledoval o pád do vývrtky. Instruktor byl připravený a zachránil přistávací manévr. Obdržel jsem poučení, že musím provést zatáčku s řádným náklonem. Nesmím mít strach v blízkosti země, že zavadím křídlem o zem. Instruktor měl v této představě o vzniku problému pravdu, ale jen částečnou. Složitost tohoto jevu jsem si uvědomil až mnohem později.
Vection iluze
Riziko létání v malé výšce překvapivě souvisí s jednou z letových iluzí, která se anglicky jmenuje “vection illusion”. Nemáme pro ní v češtině výstižné pojmenování a opisem bych ji pojmenoval “iluze zdánlivého pohybu”. Vzorovou situaci jsme jistě zažili už všichni. Sedíte ve vlaku, podíváte se z okna a vidíte pomalu se rozebíhající obrysy vlaku, který stál na vedlejší koleji. Paráda, už jedeme, říkáte si. Zklamání přichází v okamžiku, kdy si uvědomíte, že ve skutečnosti se rozjel vlak vedle vás. Právě jste podlehli vection iluzi.
Tuto historku můžu vyprávět i jinak. Jedete autem do mírného kopce a zastavíte na červenou na semaforu. Náhle máte pocit, že se vaše auto samovolně rozjíždí dopředu a začnete dupat do brzdy, abyste nenarazili do auta stojícího před vámi. Ve skutečnosti stojíte, to auto stojící před vámi začalo pomalu couvat...
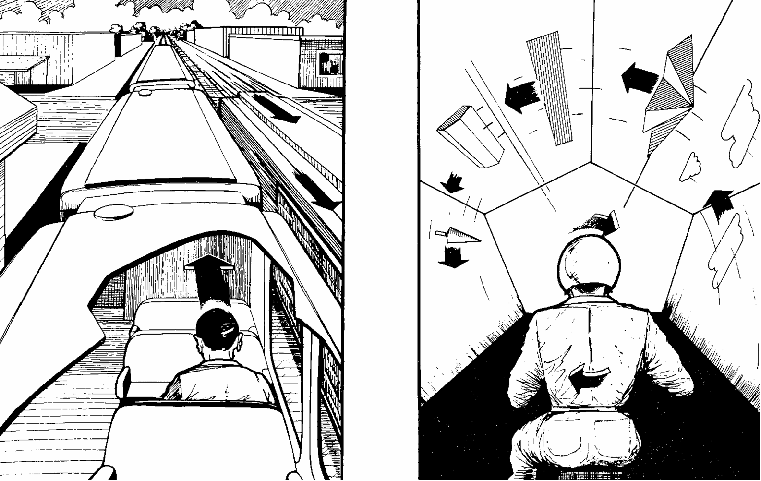
Popsali jsme si lineární vection iluzi, vlak se pohybuje lineárně. Podobně je definována radiální vection iluze využívaná často v elektronicky simulované virtuální realitě. Pokud jste v uzavřeném prostoru a okolí kolem vás se začně otáčet, aniž byste měli v zorném poli pevný bod, budete mít subjektivní pocit, že se otáčíte pouze vy sami a to v opačném směru, viz obrázek níže.
Pokud budete studovat odbornou literaturu pro piloty, o vection iluzi toho mnoho nenajdete. Běžně se dočtete, že vás může potkat při pojíždění s letadlem po letišti. Mezi aerolubovými příběhy jsem zaznamenal vyprávění dopravního pilota, který se vracel do kokpitu pro zapomenuté sluneční brýle přesně ve chvíli, kdy na vedlejší stojánce začal pushback letadla. Podlehl vection iluzi a měl poct, že se letadlo odstavené na špalcích rozjíždí. Začal intenzivně šlapat na brzdu, která nemohla být bez tlaku v hydraulickém systému účinná. Je to sice zajímavá historka, ale bylo to na stojánce a to přece není žádná pořádná letová iluze. Ve skutečnosti je výskyt této iluze za letu častý a může nás přivést do nebezpečné situace.
Nyní se vrátím zpět do svého větroně. Předpokládejme, že letím dlouhý termický let ve velké, pohodlné výšce.
- Země je daleko, krajina ubíhá pode mnou pomalu a rychlost letadla subjektivně vnímám jako velmi pomalou. Kolem mne je pouze vzduch a já nevidím nic, proti čemu bych mohl pozorovat svoji skutečnou rychlost. Podléhám mírné lineární vection iluzi, která snižuje moje vnímání rychlosti letadla.
- Nyní točím ve stoupavém proudu zatáčku o náklonu 45 stupňů. Pohledem z okénka nemám možnost vnímat skutečný poloměr zatáčky, protože v blízkosti letadla není pevný bod, proti kterému bych mohl srovnat poloměr otáčení. Mám subjektivně pocit, že se letadlo otáčí prakticky na místě kolem svého těžiště. To je mírná radiální vection iluze.
- Když se v zatáčce podívám z kabiny na konec křídla mířícího do středu zatáčky, krajina ubíhá pomalu dopředu, ale konec křídla couvá dozadu. Pohyb krajiny se sčítá s pohybem křídla a přispívá k pocitu, že s letadlem létám ladné zatáčky o malém poloměru. Ve větroni je tento jev umocněn tím, že pilot sedí před těžištěm letadla.
Po několikahodinovém letu termika končí a já ztrácím výšku. Musím přistát na neznámé letiště nebo do terénu. Vidím přistávací plochu a dělám si rozpočet. Přistávám na neznámém místě, ve kterém nemám vypozorovné obvyklé body a výšky pro otáčení okruhových zatáček. Čtvrtou závěrečnou zatáčkou se dotáčím do osy dráhy asi v padesáti až sto metrech výšky. Země je blízko a opačná vection iluze se dostavuje v mnohem zákeřnější podobě.
- Při prakticky stejné dopředné rychlosti letadla kolem mě země opticky náhle ubíhá mnohem rychleji. Subjektivně mám pocit značného nárůstu rychlosti a svádí mě to k přitahování a zpomalování. To je agresivní lineární vection iluze, ale v opačném směru, než ve velké výšce.
- Ačkoli zatáčku provádím s přiměřeným náklonem, díky blízkosti země mám optický pevný bod a náhle vnímám skutečný velký poloměr zatáčky větroně. Dřívější radiální vection iluze odezněla. Mám snahu letoun umravnit a obnovit jeho ochotu k otáčení vyšlápnutím nožního řízení.
- Když se podívám na konec křídla, to už neustupuje dozadu jako ve velké výšce, ale naopak svižně ubíhá krajinou dopředu. To dál zvyšuje dojem neochoty letadla k zatáčení a nutí mě to k dalšímu vyšlápnutí nožního řízení.
- Náhle vidím, že původní rozpočet ovlivněný nesprávným vnímáním manévrů ve velké výšce selhává, zatáčku přetočím a jsem nucen se další esovitou zatáčkou vrátit do osy dráhy. Současně doufám, že ze země nikdo nevidí moje letecké umění. Rozpočet selhal v blízkosti země, čímž jsem vytvořil potencionálně nebezpečnou situaci.
- Pokud se v okolí přistávcí dráhy vyskytuje kopec, začne vám zvyšovat falešný horizont. V zatáčce máte v zorném poli více země a méně oblohy. To subjektivně navozuje vnímání většího náklonu letadla, než je ve skutečnosti.
Nyní shrnu následky vection iluze v blízkosti země. V blízkosti země ve čtvrté zatáčce mám tendenci přitahováním řídící páky zpomalovat. Současně mám potřebu více vyšlapovat nožní řízení a snižovat náklon. Zatáčka je výkluzová. Na vývrtku je v takové situaci zaděláno. Tato iluze si již vybrala daň v podobě mnoha lidských životů. Příklad takové nehody je zachycen níže.
Vection iluze za letu je způsobena tím, že v bezprostřední blízkosti letadla nemám možnost pozorovat pevný bod, který by mi umožnil správně vnímat svoji rychlost a poloměr zatáčky. Funguje to úplně stejně nejen pro větroně, ale pro všechny ostatní létající aparáty včetně těch nejjednodušších. To vše platí ale jen do okamžiku, kdy se přiblížím nebo vletím do oblačnosti. Pozorování blízkého mraku, který je vzhledem k rychlosti letadla prakticky v klidu vůči zemi a vytváří pevný bod pro pozorování, subjektivně vnímám jako náhlý prudký nárůst rychlosti. Když letadlo úmyslně vlétá do oblačnosti při letu podle přístrojů, piloti mají tendenci zpomalovat a stahovat plyn. Vzniká zde riziko pádu letadla.
Vection iluze může mít i jiné nečekané podoby. Vletím s letadlem do deště. Když má moje letadlo čelní štítek přibližně kolmý k zemi, kapky stékající v dešti po štítku budou ubíhat směrem dolů. Pozorováním kapek může vzniknout vection iluze. Máte subjektivní pocit, že kapky jsou v klidu, ale letadlo stoupá. Pokud se štítek kabiny blíží vodorovné poloze, kapky budou ubíhat dozadu a v děšti budete mít nesprávný pocit, že letadlo klesá.
Piloti vrtulníků znají jinou zákeřnou situaci. Když startují v prašném prostředí, kolem vrtulníku se vytváří otáčivé proudění vzduchu. Rotor nasává vzduch z okolí a vrhá jej proti zemi. Tam proud vzduchu víří prach, který je znovu nasáván do rotoru. Pokud je prachu hodně a pilot zdratí optický kontakt s horizontem, vidí pouze prach proudící proti zemi. Subjektivně díky lineární vection iluzi vznikne pocit, že vrtulník prudce stoupá a nesprávným zásahem do kolektivu pilot přivede vrtulník tvrdě zpět na zem.
Otočná výška
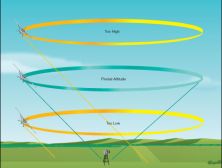
Nyní se ale opět vrátím do svého větroně. Pozorný čtenář si všimnul, že v zatáčce ve velké výšce se na vection iluzi podílí geometrický jev, kdy při pohledu z kabiny do středu zatáčky konec křídla ustupuje dozadu. Naopak v malé výšce ubíhá svižně dopředu. Logicky někde musí být správná výška, ve které konec křídla směřuje spořádaně do bodu, kde osa otáčení protíná zemi a konec křídla se zdánlivě proti zemi nepohybuje.
Tento problém v letectví řešíme poměrně často. Představte si, že vezete své přátele na vyhlídkový let nad Karlštejn. Chcete, aby si vyhlídkový let užili a chcete ustředit zatáčku v takové vzdálenosti a s takovým náklonem, aby Karlštejn zůstával v zorném poli ve středu otáčení letadla. Po chvíli překvapivě zjistíte, že je to nemožné a pokud letíte správně ustředěnou zatáčku, Karlštejn vám vždycky uteče nejdříve ze středu otáčení a potom i ze zorného pole a schová se pod vás. Jste nucení měnit náklon, kličkovat a znovu jej lovit do zorného pole. To si potom říkáte, co si vaši přítelé asi pomyslí o vašem leteckém umění.
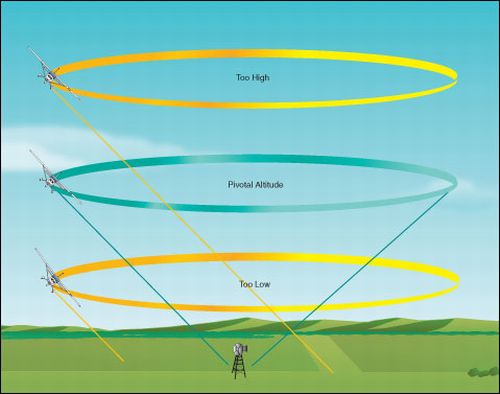
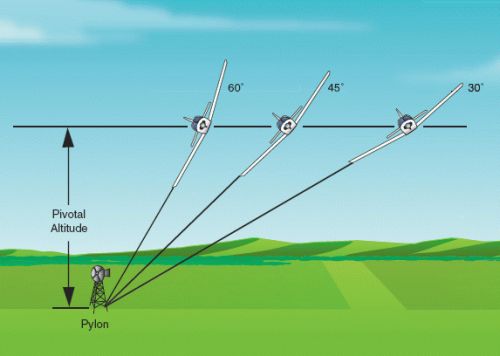
Matematické řešení situace je poměrně překvapivé. Pro vaše letadlo letící určitou cestovní rychlostí existuje pouze jedna výška, ve které je možné letět takovou zatáčku, aby Karlštejn způsobně zůstal na konci křídla v ose otáčení letadla. V anglické odborné literatuře se tato výška označuje jako “pivotal altitude” a české synonymum pro tento pojem jsem nenašel a pravděpodobně neexistuje. Nazvěme ji “otočnou výškou”. Definujme ji jako výšku, ve které se letadlo letící danou rychlostí otáčí tak, že osa pohledu kolmo do zatáčky směřuje do pevného bodu na zemi. Důležitá informace je, že otočná výška není závislá na náklonu ani na vzdálenosti od osy otáčení. Otočná výška je závislá pouze na rychlostí letadla.
Jsem si vědom toho, že přítomnost každé rovnice v článku snižuje počet čtenářů na polovinu, ale tentokrát to za to určitě stojí:
otočná výška = (rychlost vůči zemi x rychlost vůči zemi) / 11,3
Rychlost vůči zemi (GS) si dosaďte v uzlech, otočná výška vyjde ve stopách nad zemí (AGL). Podrobnosti najdete zde: http://www.norcalflight.com/pdfs/commercial/CPFL_Eights_on_Pylons.pdf.
|
rychlost GS (uzly) |
otočná výška AGL (stopy) |
|
60 |
319 |
|
65 |
374 |
|
70 |
434 |
|
75 |
498 |
|
80 |
566 |
|
85 |
639 |
|
90 |
717 |
|
95 |
799 |
|
100 |
885 |
|
105 |
976 |
|
110 |
1071 |
|
115 |
1170 |
|
120 |
1274 |
To znamená, že pokud chcete udžet Karlštejn na konci křídla, musíte najít nikoli správný náklon v zatáčce, ale správnou výšku! Otočná výška exponenciálně narůstá s rychlostí letadla. Jestliže se běžné ultralehké letadlo pohybuje cestovní rychlostí třeba přibližně 100 uzlů, otočná výška se blíží 900 ft, což je obvyklá výška, ve které je možné letět vyhlídkový let. V tabulce vpravo je přehled rychlostí a odpovídajících otočných výšek.
Uvedená fakta samozřejmě platí pouze za bezvětří. V té části manévru, kde vítr fouká v ose pohybu letadla a letadlo urychluje nebo zpomaluje proti zemi, mění se otočná výška a my musíme měnit výšku letadla (nikoli náklon!) tak, abychom účinek větru eliminovali. V té části trajektorie, kde fouká boční vítr, musíme jeho snos vylučovat náklonem. Současně s bočním větrem bude kolísat vzdálenost od otočného bodu. Na návětrné straně se budeme k otočnému bodu přibližovat a zvyšovat náklon. Po větru od otočného bodu se budeme vzdalovat od otočného bodu a náklon se bude snižovat. Takový manévr není snadný a zatáčky musí bát především správně ustředěné bez výkluzu a skluzu.
Podle osnov amerického Federálního leteckého úřadu jsou povinni budoucí obchodní piloti a instruktoři takový manévr nacvičovat a zvládnout. Úlohou je létát ležatou osmičku kolem dvou konstatních bodů v otočné výšce tak, aby se otočné body nepohybovaly.
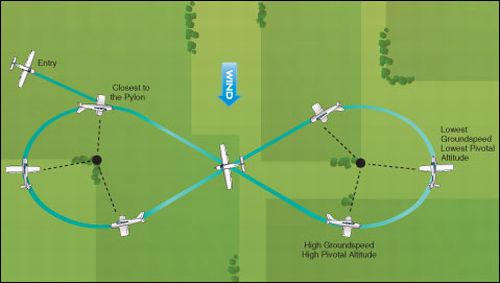
Na nácvik máte jednu letovou hodinu. Nejprve si nalétnete správnou otočnou výšku. Nyní musíte vylučovat vítr tak, že při pohybu otočného bodu dopředu musíte potlačit řídící páku a klesat. Při pohybu otočného bodu dozadu musíte přitáhnout řídící páku a stoupat. Při nácviku je nutné předvídat pohyby a reagovat jemnými změnami výšky. Se změnou vzdálenosti od otočného bodu se účinkem větru bude měnit i potřebný náklon, otočný bod ale musí zůstat v ose křídla.
Důležité je nesnažit se udržet Karlštejn nožním řízením a létat správně ustředěné zatáčky. Takový nácvik je vysokou školou létání. Lze jej samozřejmě provádět i v létajících aparátech bez křídel, jako třeba v motorovém paraglide. Jen si chybějící křídlo je třeba představit. Správně provedený manévr je možné vidět níže.
Hlavním poučením pro nás je fakt, že v malé výšce v blízkosti země se mění vnímání rychlosti, náklonu a poloměru zatáček. Blízkost země svádí k provádění výkluzových zatáček a narušuje správný rozpočet pro přistání podhodnocením poloměru zatáčky potřebné pro srnovnání letadla do osy dráhy. Riziko je největší po déle trvajícím letu ve velké výšce a při přistávání na neznámém letišti nebo do terénu.
Jako u všech letových iluzí, znalosti a zkušenosti nesnižují riziko vzniku tohoto fenoménu, ale dávají nám větší šanci nebezpečí rozeznat a řešit.